Minimum mean square error
In statistics and signal processing, a minimum mean square error (MMSE) estimator describes the approach which minimizes the mean square error (MSE), which is a common measure of estimator quality.
The term MMSE specifically refers to estimation in a Bayesian setting, since in the alternative frequentist setting there does not exist a single estimator having minimal MSE. A somewhat similar concept can be obtained within the frequentist point of view if one requires unbiasedness, since an estimator may exist that minimizes the variance (and hence the MSE) among unbiased estimators. Such an estimator is then called the minimum-variance unbiased estimator (MVUE).
Contents |
Definition
Let  be an unknown random variable, and let
be an unknown random variable, and let  be a known random variable (the measurement). An estimator
be a known random variable (the measurement). An estimator 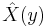 is any function of the measurement
is any function of the measurement  , and its MSE is given by
, and its MSE is given by
where the expectation is taken over both  and
and  .
.
The MMSE estimator is then defined as the estimator achieving minimal MSE.
In many cases, it is not possible to determine a closed form for the MMSE estimator. In these cases, one possibility is to seek the technique minimizing the MSE within a particular class, such as the class of linear estimators. The linear MMSE estimator is the estimator achieving minimum MSE among all estimators of the form 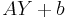 . If the measurement
. If the measurement  is a random vector,
is a random vector,  is a matrix and
is a matrix and  is a vector. (Such an estimator would more correctly be termed an affine MMSE estimator, but the term linear estimator is widely used.)
is a vector. (Such an estimator would more correctly be termed an affine MMSE estimator, but the term linear estimator is widely used.)
Properties
- Under some weak regularity assumptions,[1] the MMSE estimator is uniquely defined, and is given by
-
- In other words, the MMSE estimator is the conditional expectation of
 given the observed value of the measurements.
given the observed value of the measurements.
- If
 and
and  are jointly Gaussian, then the MMSE estimator is linear, i.e., it has the form
are jointly Gaussian, then the MMSE estimator is linear, i.e., it has the form 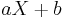 for constants
for constants  and
and  . As a consequence, to find the MMSE estimator, it is sufficient to find the linear MMSE estimator. Such a situation occurs in the example presented in the next section.
. As a consequence, to find the MMSE estimator, it is sufficient to find the linear MMSE estimator. Such a situation occurs in the example presented in the next section.
- The orthogonality principle: An estimator
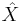 is MMSE if and only if
is MMSE if and only if
-
- for all functions
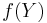 of the measurements. A different version of the orthogonality principle exists for linear MMSE estimators.
of the measurements. A different version of the orthogonality principle exists for linear MMSE estimators.
Example
An example can be shown by using a linear combination of random variable estimates 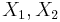 and
and 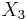 to estimate another random variable
to estimate another random variable 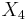 using
using 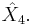 If the random variables
If the random variables ![X=[X_{1}, X_{2},X_{3},X_{4}]^{T}](/2012-wikipedia_en_all_nopic_01_2012/I/9bb903c4cdc3a75c001ae63051200a43.png) are real Gaussian random variables with zero mean and covariance matrix given by
are real Gaussian random variables with zero mean and covariance matrix given by
we will estimate the vector 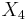 and find coefficients
and find coefficients 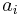 such that the estimate
such that the estimate 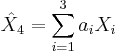 is an optimal estimate of
is an optimal estimate of 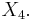 We will use the autocorrelation matrix, R, and the cross correlation matrix, C, to find vector A, which consists of the coefficient values that will minimize the estimate. The autocorrelation matrix
We will use the autocorrelation matrix, R, and the cross correlation matrix, C, to find vector A, which consists of the coefficient values that will minimize the estimate. The autocorrelation matrix  is defined as
is defined as
The cross correlation matrix  is defined as
is defined as
In order to find the optimal coefficients by the orthogonality principle we solve the equation 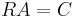 by inverting
by inverting  and multiplying to get
and multiplying to get
So we have 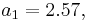
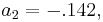 and
and 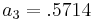 as the optimal coefficients for
as the optimal coefficients for 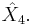 Computing the minimum mean square error then gives
Computing the minimum mean square error then gives ![\left\Vert e\right\Vert _{\min}^{2}=E[X_{4}X_{4}]-C^{T}A=15-C^{T}A=.2857](/2012-wikipedia_en_all_nopic_01_2012/I/af28acfe0aa0d7bcccac23d2c4397238.png) .[2]
.[2]
A shorter, non-numerical example can be found in orthogonality principle.
See also
- Bayesian estimator
- Mean squared error
- Minimum-variance unbiased estimator (MVUE)
- Orthogonality principle
Notes
Further reading
- Johnson, D. (22 November 2004). Minimum Mean Squared Error Estimators. Connexions
- Prediction and Improved Estimation in Linear Models, by J. Bibby, H. Toutenburg (Wiley, 1977). This book looks almost exclusively at minimum mean-square error estimation and inference.
- Jaynes, E. T. Probability Theory: The Logic of Science. Cambridge University Press, 2003.
- Lehmann, E. L.; Casella, G. (1998). Theory of Point Estimation. Springer. pp. 2nd ed, ch. 4. ISBN 0-387-98502-6.
- Kay, S. M. (1993). Fundamentals of Statistical Signal Processing: Estimation Theory. Prentice Hall. pp. 344–350. ISBN 0-13-042268-1.
- Moon, T.K. and W.C. Stirling. Mathematical Methods and Algorithms for Signal Processing. Prentice Hall. 2000.
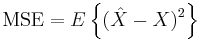
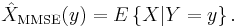
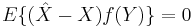
![\operatorname{cov}(X)=E[XX^{T}]=\left[\begin{array}{cccc}
1 & 2 & 3 & 4\\
2 & 5 & 8 & 9\\
3 & 8 & 6 & 10\\
4 & 9 & 10 & 15\end{array}\right],](/2012-wikipedia_en_all_nopic_01_2012/I/74fe8ab98cdcd35183e0763cf5007e6a.png)
![R=\left[\begin{array}{ccc}
E[X_{1},X_{1}] & E[X_{2},X_{1}] & E[X_{3},X_{1}]\\
E[X_{1},X_{2}] & E[X_{2},X_{2}] & E[X_{3},X_{2}]\\
E[X_{1},X_{3}] & E[X_{2},X_{3}] & E[X_{3},X_{3}]\end{array}\right]=\left[\begin{array}{ccc}
1 & 2 & 3\\
2 & 5 & 8\\
3 & 8 & 6\end{array}\right].](/2012-wikipedia_en_all_nopic_01_2012/I/09db2050c61c55657a656287f5e73601.png)
![C=\left[\begin{array}{c}
E[X_{4},X_{1}]\\
E[X_{4},X_{2}]\\
E[X_{4},X_{3}]\end{array}\right]=\left[\begin{array}{c}
4\\
9\\
10\end{array}\right].](/2012-wikipedia_en_all_nopic_01_2012/I/24938c715e08c576ef45ed6c86c902f7.png)
![R^{-1}C=\left[\begin{array}{ccc}
4.85 & -1.71 & -.142\\
-1.71 & .428 & .2857\\
-.142 & .2857 & -.1429\end{array}\right]\left[\begin{array}{c}
4\\
9\\
10\end{array}\right]=\left[\begin{array}{c}
2.57\\
-.142\\
.5714\end{array}\right]=A.](/2012-wikipedia_en_all_nopic_01_2012/I/946df5eac42c6da0a5b6d53c41d0a745.png)